
أبن الهيثم في الرياضيات

لقد أيقن أبن الهيثم ان التحليل والتركيب هما الغاية التي ينتهي اليها كل باحث، وفي نظره فإن التحليل هو القياس والتركيب هو البرهان يقول في "التحليل والتركيب ما نصه (مخطوط بدار الكتب 323 رياضيات تيمور)
"كل علم وكل تعلم فله غاية هي ذروته التى يسعى إليها المجتهدين، وعلوم التعاليم مبنية على البراهين، وغاياتها هي أستخراج المجهولات من جزئياتها، ووجود البراهين التي تدل على خصائصها ومعانيها.
والدورة التي تسمو إليها في هذه العلوم، والمجتهدين لطلبها، الظفر بالبراهين، التي تستنبط بها مجهولاتها، والبرهان الدال بالضرورة على صحة نتيجته، وهذا القياس هو مركب من مقدمات تعرف فيها، ومن نظام وترتيب لهذه المقدمات، وطريق هذه المقاييس هو تصيد مقدماتها، وتحمل الحيل في ثقة أليها. والصناعة التي تصيد هذه المقدمات، وبها يتوصل إلى الترتيب المؤدي إلى المطلوب من نتائجها يسمى صناعة التحليل، وجميع ما خرج الى الوجود من علوم التعاليم أنما خرج بهذه الصناعة".
ومن طرق القياس يمكن استخراج المجهول من جزيئات الظواهر الفيزيقية التي تقع للحس، أو من المعطيات الحسابية والرياضية، فالعلوم في حالة كهذه ليست إلا من نتاج العقل البشري، فالعلوم غير كامنة كمون الشرر في الحجر، بل هي تخرج إلى الوجود بالتحليل، وهو القياس، ثم بالتركيب وهو البرهان، طبقا لمفاهيم العصر، وقد يعتروها التبديل والتغيير خصوصا في الفلك والطبيعات فتتمسح بمسحات محدثة من مفاهيم عصر أخر.
والقياس هذا في نظر ابن الهيثم هو قول مؤلف من اقوال إذا سلمت لزم عنها لذاتها شيء أخر، فهو يعتمد على علاقة الاشتمال، ويطبقه في الطبيعيات وأهمها الضوء والفلك، كما يطبقه في الرياضيات والهندسة.والواضح ان منحى أبن الهيثم في التحليل يقارب منحى" ديكارت" الذي أورد ذكره في "مقال في المنهج" حيث أوصى في القاعدة الثانية بأن "أقسم كل واخدة من المعضلات التي سأختبرها إلى أجزاء بقدر ما في الوسع، وبقدر ما تدعوا الحاجة على خير الوجوه".
هذا التحليل في الهندسيات ويوصل الى نتائج حاسمة لا تباين بينها، أما التحليل في الطبيعيات فقد يؤدي إلى نتائج سيالة حسب تعبير أبن الهيثم، أي إلى نظريتين أو أكثر لكل منها فئة تؤيدها وتعضدها.
مسألة لأبن الهيثم:
كل ضلعين من مثلث فهما اعظم من الضلع الباقي.
أن تطبيق أبن الهيثم فكرة التحليل والتركيب في هذه المسألة فيه ابعاد تستوعب العمق في المنحى الفكري، بل تطبيقه على قضايا أخر في الطبيعيات وفي علم الضوء قد ابرز نقاطا على جانب كبير من الاهمية، يقول ابن الهيثم:
"فتحليل هذا الشكل هو أن نفرض الدعوى على ما أوحى فيها، فيكونا ضلعا "أ ب ، أ ح" مجموعتين اعظم من "ب ح" ".
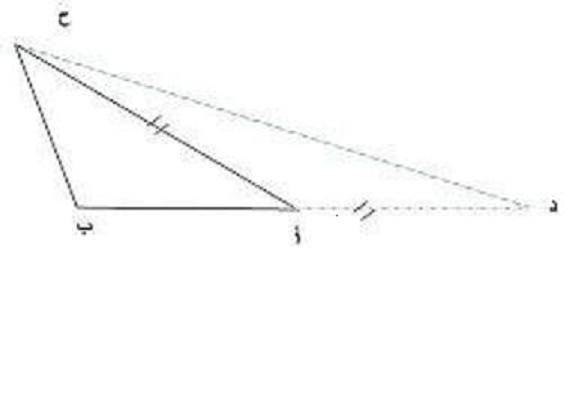
يفترض أبن الهيثم وجود المثلث حسب الشكل الأتي، وذلك في مثاله الهندسي الذي اخضعه للتحليل والتركيب. ويقول أبن الهيثم في التحليل والتركيب: "فتحليل هذا الشكل هو ان نفرض الدعوى على ما اوحى فيها، فيكونا ضلعي أ ب ، أ ح مجموعتين أعظم من ب ح فننظر في خواص المثلث ليظهر فيها خاصة تؤدي إلى ذلك، وإذا نظر في خواص المثلث وهو على ما هو عليه لم يوجد فيه خاصة تؤدي إلى صحة هذه الدعوى، فينبغي ان يحدس المحلل على زيادة يزيدها في هذا الشكل ليحدث بها خاصة أو خواص ليست موجودة في هذا المثلث، وهو على ما هو عليه واجد الزيادات التي تحتمل أن تزاد لتحدث خاصة زايدة. هو ان نجعل الضلعين خطا واحدا فنخرج ب أ على أستقامة، ونفصل منه مثل أ ح وليكن أ، فيكون ب د أعظم من ضلع ب ح.
نصل ح د فيصبح ب د ح مثلثا، ويكون ضلع د ب منه اعظم من ضلع ب ح، فقد تبين في الشكل الثامن عشر من المقال الاولى من كتاب "أوقليدس" أن الضلع الاعظم من كل مثلث يوتر الزاوية العظمى، فتكون زاوية ب ح د أعظم من زاوية ب د ح.
ولكن زاوية ب ح د لأن أ د = أ ح.
فتكون الزاوية ب ح د أعظم من الزاوية أ ح د.
ولأن الأمر كذلك، فقد أنتهى التحليل إلى معنى هو معطى لا شك فيه، وهو ان زاوية ب ح د أعظم من زاوية أ ح د. وتركيب هذه المسألة يكون كما نصف:
نخرج ب أ على استقامة كما فعل في التحليل، ونفصل أ د مثل أ ح.
ونصل د ح فيكون زاوية ب ح د أعظم من زاوية أ ح د.
هذه المقدمة هي التير توصل أليها التحليل، وهي التي تجعل أ د أوله في البرهان،
ويكون ضلع ب د أعظم من ضلع ب ح.
كما تبين في الشكل التاسع عشر من المقال الأول من كتاب "أوقليدس" وضلع ب د هو مثل الضلعين أ ب + أ ح.
وعليه فضلعا ب أ + أ ح أعظم من ضلع ب ح، وذلك ما أردنا أن نبين"
ولقد اكتشق العديد من المخطوطات التي تنسب لأبن الهيثم والتي كانت أساسا لعدت نظريات رياضية حول خصائص المثلث والكرة، وكيفية استخراج ارتفاعات الأجسام، وغير ذلك
مجموع سلسلتي القوى الثاثلة والرابعة للأعداد الطبيعية:
قد اوجد أبن الهيثم مجموع سلسلتي القوى الثاثلة والرابعة للأعداد الطبيعية ، عندما كان يقوم بحساب الجسم الدوراني الناتج عن دوران قطعة قائمة من قطع مكافئ حول محور عمودي على محور تماثلها.
على غرار ما يلي بالرموز الجبرية الحديثة:
![]()
![]()
وهذا المجموع هو حل تقريبي للتكامل